法线贴图（凹凸映射 Bump Mapping ） ​

简介 ​

今天我们学习的内容是法线贴图，法线贴图也是贴图的一种。在法线贴图中，储存了每个像素点的法线方向。（法线方向用 x,y,z 表示，贴图中的 r,g,b 三个通道正好可以表示）。

动机 ​

法线贴图通常使用在一些模型精度不是很高，但是需要展示更多细节的地方。比如，我们需要渲染一面砖墙。我们当然可以在建模工具中将每一块的砖的顶点数据都表示出来，但是这样做的代价就是巨大的人工成本。而使用法线贴图则可以将砖墙的法线存储在一张图片中，在渲染时再进行计算。

观察下面两张图片（左侧为没有应用法线贴图，右侧应用了法线贴图），我们可以发现应用了发现贴图的立方体更加显得有凹凸感。而我们却没有对模型的顶点做出任何的修改。这就是法线贴图的便利之处。

法线贴图的类型 ​

法线贴图中存储的是物体的法线方向，由于法线方向处于[-1, 1]的范围之间，而像素颜色的 RGB 则处于[0,1]之间。那么我们需要做一个映射，不难得出下面的公式：

$$color = \frac{normal + 1}{2}$$

$$normal = color \times 2 - 1$$

有了上面的基础理论，我们还面临另一个问题，我们的法线是存储在哪个坐标空间中呢？首先我们联想到的就是存储在模型空间中。

模型空间法线贴图 ​

顾名思义，模型空间的法线贴图就是这些法线坐标都是以模型空间为基准生成的。模型空间下的法线贴图有以下的优点：

1. 实现简单，非常直观。我们都不需要模型的原始法线和切线信息，生成模型空间的法线贴图也非常的简单。
2. 在纹理坐标的缝合处和尖锐的边角部分，可见的突变较少，即可以提供平滑的边界。

但是法线贴图有一些缺点：

1. 不可重用，比如在一个立方体中我们要给每个面都贴上法线贴图的话，那么对于模型空间的法线贴图，我们需要“6”张不同的贴图。（这里的 6 加上引号是因为这 6 张图也可以合并为 1 张大图表示）
2. 不可压缩，因为模型空间下需要完整的使用 rgb 三个分量的值，所以没有压缩的空间了。

但当前业界中，更常用的是另一种法线贴图：切线空间的法线贴图。

切线空间法线贴图 ​

什么是切线空间 ​

切线空间的坐标系的 z 轴是模型的原始法线方向，x 轴是顶点的切线(Tangent)方向。这个切线方向我们暂时可以理解为是沿着纹理坐标的 u 轴方向。切线空间坐标系的 y 轴被称为副切线(BiTangent),它等于法线与切线的叉乘。如下图所示，x 轴为切线方向，y 轴为副切线方向，z 轴为法线方向。为了与模型空间的 x,y,z 轴区分，我们通常将其称为 T(Tangent),B(Bitangent),N(Normal)。切线空间的矩阵也称为 TBN 矩阵。

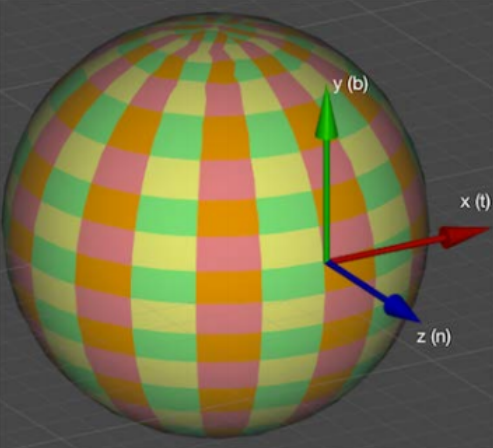
为什么是切线空间 ​

其实法线无论存储在哪个坐标系中都是可以，甚至可以选择存储在世界空间下。但是存储法线不是目的，后续的光照计算才是重点！我们引入切线空间，我们还需要将法线坐标从切线空间转换到世界中间中才能够与世界空间中的光线进行运算（或者将世界空间的坐标转换到切线空间中）。但是使用切线空间坐标系有着诸多的有点：

1. 切线空间中记录的法线信息是相对信息，这意味着即便把该法线纹理应用另一个完全不同的网格上，也可以得到一个相对合理的结果。
2. 可重用法线纹理，比如之前举例的立方体，在模型空间下我们需要使用“6”张法线纹理，但是在切线空间下，我们完全使用 1 张法线纹理就可以了。
3. 可压缩，因为切线空间下的法线纹理 z 方向总是正方向，因此我们可以仅仅只存储切线和副切线的信息，再通过叉乘来计算出法线坐标

实践 ​

说了这么多，让我们开始实践吧！

在之前的文章中我们已经介绍了如何在 Three.js 之中使用自定义的 Shader,我们就从编写 Shader 部分开始吧！

首先编写顶点着色器的部分：

顶点着色器 ​

varying vec3 vNormal;
varying vec2 vUv;
void main () {
    vUv = uv;
    vec3 transformedNormal = normalMatrix * vec3(normal);
    vNormal = normalize(transformedNormal);

    vec4 mvPosition = vec4(position, 1.0);
    mvPosition = modelViewMatrix * mvPosition;
    gl_Position = projectionMatrix * mvPosition;
}

在上面的代码中，出现了一些“未定义”的变量，比如：normal, normalMatrix, position, modelViewMatrix, projectionMatrix。其实这些变量并不是未定义，而是因为我们编写的 Shader 还不是最终的 shader 代码，Three.js 还会对我们的代码进行一系列的处理，比如增加一些预制的 attribute 和 uniform 变量，替换include的部分，替换宏等等。

其中，position与 normal是 Three.js 内置的 attribute 变量。

normalMatrix, modelViewMatrix, projectionMatrix是 Three.js 内置的uniform变量。它们的含义分别如下：

• normalMatrix: 法线矩阵，将模型空间的法线坐标转换到相机空间中
• modelViewMatrix: 模型相机矩阵，将模型空间的法线坐标转换到相机空间中
• projectionMatrix: 投影矩阵，将相机空间的坐标转换到 NDC (Normal Device Coordinates) 空间。

另外，在主函数的上方，我们还额外的声明了两个varying变量，vNormal与 vUv，因为这两个变量会在片元着色器中使用，所以我们需要使用varying关键字来修饰它们。

片元着色器 ​

接下来就是编写片元着色器的部分了：

varying vec3 vNormal;
varying vec2 vUv;

void main() {
    vec3 normal = normalize(vNormal);
    gl_FragColor = vec4(normal, 1.0);
}

在上面的代码中，我们声明了与顶点着色器中相同的变量vNormal与vUv。这是 GLSL 中一种固定的写法，可以理解为这样我们就可以使用顶点着色器传递过来的值了。

除此之外，我们还需要声明两个纹理变量mainTex与 normalTex，它们分别表示主纹理与法线纹理。

我们先检验一下上述的 shader 代码是否正确。如果代码正确的话，会得到如下的结果。

接下来我们需要往我们的 shader 中引入两张贴图，分别是主纹理mainTex与法线纹理normalTex，我们需要在片元着色器中声明 uniform 变量，其类型为sampler2D

varying vec3 vNormal;
varying vec2 vUv;
uniform sampler2D mainTex; 
uniform sampler2D normalTex; 

void main() {
    vec4 normalColor = texture(normalTex, uv); 
    vec4 mainColor = texture(mainTex, uv); 
    vec3 normal = normalize(vNormal);
    gl_FragColor = vec4(mainColor, 1.0);
}

除此之外，在 js 代码中，我们还需要在 new ShaderMaterial中传入uniform参数。我们可以利用TextureLoader来加载纹理，也可以直接 new Texture来创建纹理，但是有一点需要注意的是我们需要将纹理(Texture)的 needsUpdate属性设为true。

const loader = new TextureLoader();
const mat = new ShaderMaterial({
    vertexShader: normalVert,
    fragmentShader: normalFrag,
    uniforms: {
        mainTex: {
            value: loader.load(mainTexURL),
        },
        normalTex: {
            value: loader.load(normalTexURL),
        },
    },
});

做完这一步我们再次检查 shader 代码是否能够正确的渲染主纹理和法线纹理（将 gl_FragColor 分别设置为gl_FragColor=mainColor与 gl_FragColor=normalColor）。

如果修改正确会得到下面的效果。

接下来的操作就比较繁琐一点了。我们现在需要将法线贴图从切线空间转换到相机空间中。涉及到坐标系的转换我们很容易的联想到需要矩阵进行转换！没错，我们需要获取每个顶点的TBN矩阵。获取TBN矩阵则需要计算切线与副切线。如何计算切线与副切线今天我们暂且按下不表。Three.js 的Geometry类为我们提供了一个方法可以直接计算切线与副切线的方法：Geometry.computeTangents。

接下来我们需要修改顶点着色器，通过查看相关资料发现 Three.js 提供了 tangent这一内置变量，表示切线的方向。那么我们可以在顶点着色器中利用法线与切线的叉乘计算副切线的方向。再传入片元着色器中。

因此，我们还需要声明三个varying类型的变量vNormal, vTangent, vBitangent，分别表示法线、切线、副切线。

varying vec3 vNormal;
varying vec2 vUv;
varying vec3 vTangent;
varying vec3 vBitangent;
void main () {
    vUv = uv;
    vec3 transformedNormal = normalMatrix * vec3(normal);
    vNormal = normalize(transformedNormal);

    vec3 transformedTangent = (modelViewMatrix * vec4(tangent.xyz, 0.0)).xyz;
    vTangent = normalize( transformedTangent );
    vBitangent = normalize( cross( vNormal, vTangent ) * tangent.w );

    vec4 mvPosition = vec4(position, 1.0);
    mvPosition = modelViewMatrix * mvPosition;
    gl_Position = projectionMatrix * mvPosition;
}

与法线略微有些不同的是，tangent是具有 4 个分量的，tangent.w决定改了切线空间的副切线的方向性。

此时，我们再次运行代码，会发现有一个错误。

这个错误是因为我们没有在ShaderMaterial中声明USE_TANGENT的宏。所以我们需要在ShaderMaterial的参数列表中传入：

const mat = new ShaderMaterial({
    vertexShader: normalVert,
    fragmentShader: normalFrag,
    uniforms: {
        mainTex: {
            value: mainTex,
        },
        normalTex: {
            value: normalTex,
        },
    },
    defines: {
        USE_TANGENT: true, 
    },
});

接着我们修改片元着色器。在片元着色器中，我们同样需要声明三个varying变量vNormal, vTangent, vBitangent。有了这三个变量后，我们就可以构建TBN矩阵。

$$\textbf{TBN} = \begin{bmatrix} \vec t & \vec b & \vec n \end{bmatrix} = \begin{bmatrix} \vec t_x & \vec b_x & \vec n_x \\ \vec t_y & \vec b_y & \vec n_y \\ \vec t_z & \vec b_z & \vec n_z \end{bmatrix}$$

通过 TBN 矩阵，可以将切线空间的坐标转换到世界空间中：

$$\textbf p_{world} = \textbf M_{TBN} \textbf p_{tan}$$

由于在 GLSL 的 shader 代码中，矩阵是行主序的排列形式，所以 TBN 矩阵写为：

mat3 tbn = mat3(normalize(vTangent), normalize(vBitangent), normal);

我们再将图片的法线从 RGB 空间转换到 [-1, 1]区间之内。

void main() {
    vec2 uv = vUv;
    vec4 normalColor = texture(normalTex, uv);
    vec4 mainColor = texture(mainTex, uv);
    vec3 mapN = normalize(2.0 * normalColor.rgb - 1.0);

    vec3 normal = normalize(vNormal);
    mat3 tbn = mat3(normalize(vTangent), normalize(vBitangent), normal);
    normal = normalize(tbn * mapN);

    gl_FragColor = vec4(normal, 1.0);
}

运行代码，会得到如下的结果：

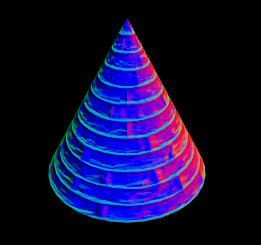
最后，我们为其完善光照，我们给其加上漫反射光照。

struct DirectionalLight {
    vec3 direction;
    vec3 color;
};
uniform DirectionalLight directionalLight;

vec3 render(DirectionalLight light, vec3 normal, vec3 diffuseColor) {
    float NdotL = clamp(dot(light.direction, normal), 0.0, 1.0);
    return diffuseColor * NdotL * light.color;
}
void main() {
    vec2 uv = vUv;
    vec4 normalColor = texture(normalTex, uv);
    vec4 mainColor = texture(mainTex, uv);
    vec3 mapN = normalize(2.0 * normalColor.rgb - 1.0);

    vec3 normal = normalize(vNormal);
    mat3 tbn = mat3(normalize(vTangent), normalize(vBitangent), normal);
    normal = normalize(tbn * mapN);

    vec3 color = render(directionalLight, normal, mainColor.rgb);

    gl_FragColor = vec4(color, 1.0);
}

与此同时，我们也需要通过 ShaderMaterial的参数列表传入光照信息，我们需要在 uniform属性中新增：

const tempVec3 = new Vector3(); 
root.getWorldDirection(tempVec3); 
const light = new DirectionalLight(0xffffff); 
light.position.x = 2; 
light.position.y = 2; 
const mat = new ShaderMaterial({
    vertexShader: normalVert,
    fragmentShader: normalFrag,
    uniforms: {
        mainTex: {
            value: mainTex,
        },
        normalTex: {
            value: normalTex,
        },
        directionalLight: {
            value: {
                direction: tempVec3, 
                color: light.color, 
            },
        },
    },
    defines: {
        USE_TANGENT: true,
    },
});

最终的渲染结果如下：

小结 ​

今天我们学习了什么是法线贴图，介绍了两种不同坐标空间下的法线贴图，在业界更常用的是切线空间下的法线贴图。另外我们还简略的介绍了 TBN 矩阵，我们利用 TBN 矩阵可以将切线空间下的坐标转换到相机空间坐标下。

总而言之，应用法线贴图的关键就 2 点：

1. 将法线贴图从 RGB 值转换到[-1, 1]的区间
2. 利用 TBN 矩阵将法线贴图的值从切线空间转换到相机空间

其实无论在切线空间计算光照还是在相机空间计算光照，最终得到的结果应该都是相同的，重点在于我们需要在同一个坐标空间下进行计算，留给读者一个问题。在切线空间下计算光照应该怎样做呢？